S Curves
I see S curves everywhere. They tell me where I should live, work, invest my time, my money, my efforts. I hope this article will help you see them too.
They appear in physics, chemistry, business, biology, animation, professional development, politics, history, memes, social media, epidemics... I made this quick video to show you some of the millions of places where they appear.
The first time I realized the ubiquity of S curves was in Pedro Domingos’s The Master Algorithm:
Most of the time, we don’t realize we’re facing S curves because they don’t look like it. We’re too close to one of their sections to realize what’s going on.
S curves are sneaky.
Early on, they look flat and we think they will never grow.
After they reach the tipping point, they look like an exponential curve and people might think they will never stop growing.
As they slow down, we think it’s the end of an S curve, forgetting a new one might be around the corner.
S curves make us miss the forest for the trees. But those who understand them early on can make millions and, in some cases, save lives. Here are a few examples of how S Curves changed the world in the last few years alone. After that, I’ll break them down to explain how you can identify them and make the most of them.
S Curves that Changed Business
Amazon’s S Curves
In Invisible Asymptotes, Eugene Wei describes how seeing Amazon as a series of S Curves converted it into a money printer.
Watch this quick video I made about Amazon’s S curves
In retrospect, it’s easy to follow Amazon’s path. But it wasn’t obvious at all three decades ago. How many online bookstores have become Amazon?
The lessons from Amazon’s S curves are clear:
If you understand S curves, you understand the potential of your business’ market size and when it will reach saturation
The best way to expand a business is expanding it through adjacencies, whether it’s new verticals (like Amazon going from books to movies and magazines), new geographies, new channels, new segments…
You can’t bet your entire business on a single bet. Eventually, you will need to figure out completely new businesses to keep growing, stacking S curves.
The best businesses figure out when they’ll reach saturation, the asymptote to their growth, before it becomes evident: while they’re still invisible asymptotes.
Facebook’s S Curves
The same thing has been true for Facebook.
How do you grow from being used by students in a campus to being used every day by two billion people? How do you go from a site where you stalk your friends to the place where you get your news? A gaming platform? How do you have the foresight to pay $1 billion for Instagram, at the time a price that was ridiculed, but which in retrospect was one of the best investments in corporate history? Every one of these steps was an S curve.
Netflix’s S Curves
Once you see these S Curves in business, you can’t unsee them.
Netflix started as DVD rentals. It had to be their first business: At the time, the incumbent was Blockbuster, which had shops where you could get movies on the spot. But you couldn’t get any movie. And you better return them quickly. So Netflix gave unlimited selection and no timelines, at the cost of having to wait a couple of days. That got them to ride their first S curve.
But waiting is not good. So they built streaming: no timelines for returns, and no waiting times, at the cost of selection, since they couldn’t get rights for all the content. That was a second S curve.
The next step was obvious: They needed no returns, no waiting times, and near infinite selection. The only way they could do that was making the content themselves. Hence Netflix Originals. Another S curve.
Now they’re only limited by the quality of their content, and that determines the limit of their current S curve. That’s why they see their competition in things like video games: They’re such an enjoyable pastime that they compete for people’s spare time. Who will prevail? The one with the highest content quality.
Coronavirus: S Curves that Changed Health
I always saw COVID as S curves. In fact, Why You Must Act Now, which gathered 40 million views, starts with 4 of them:
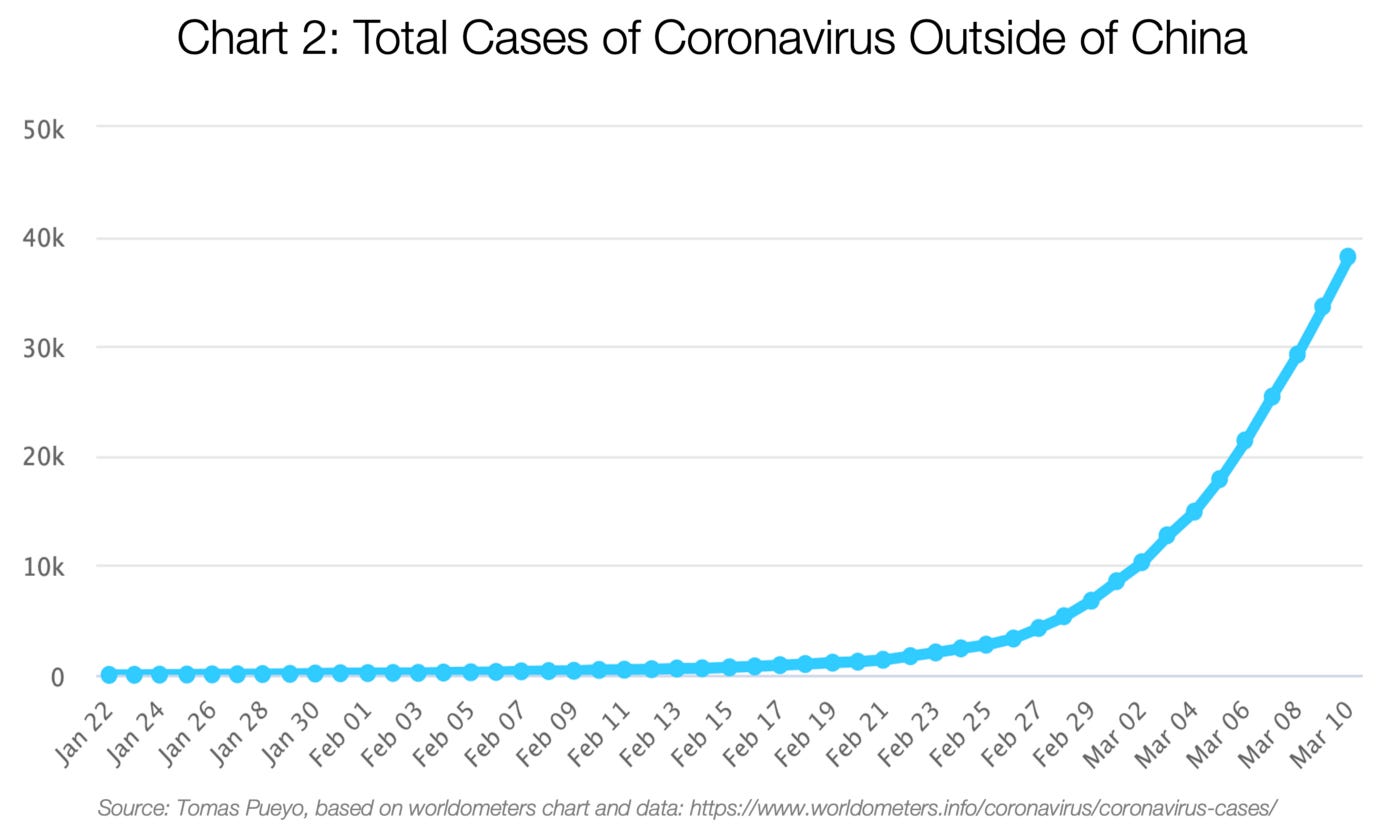
The first S curve is China’s. Here, I was alerting that we had entered a second S curve in the pandemic period.
I then extracted the second S curve to show how it was in the exponential phase:
Then I broke down this curve into its components. But the true alert came when I zoomed into the rest of the countries to show that they had already started the exponential growth phase and people were just missing it.
What I was doing, really, was just breaking down big S curves (the total new cases globally) into their component S curves (per country).
Since then, cases have just been an accumulation of S curves. In some cases, it’s more obvious than others:
That’s not the only place where COVID and S curves appeared though.
Mobility across countries followed S curves, progressing normally until they sank in March 2020, stabilizing afterwards.
And not just mobility.
The views of any article follow an S curve: First a few people see it, then they share it, more people see it, they share it again… and eventually it reaches all its potential readers and news move on to the next beat.
Business, epidemics, ideas... What fundamental laws drive S curves? How can we understand when there’s an S curve, so we can predict what happens next?
Driving S Curves
There are two parts in an S curve: acceleration and deceleration, with another phase in between.
Linear Acceleration
There’s an acceleration phase whenever something can build up speed over time, like a car moving or a process speeding up.
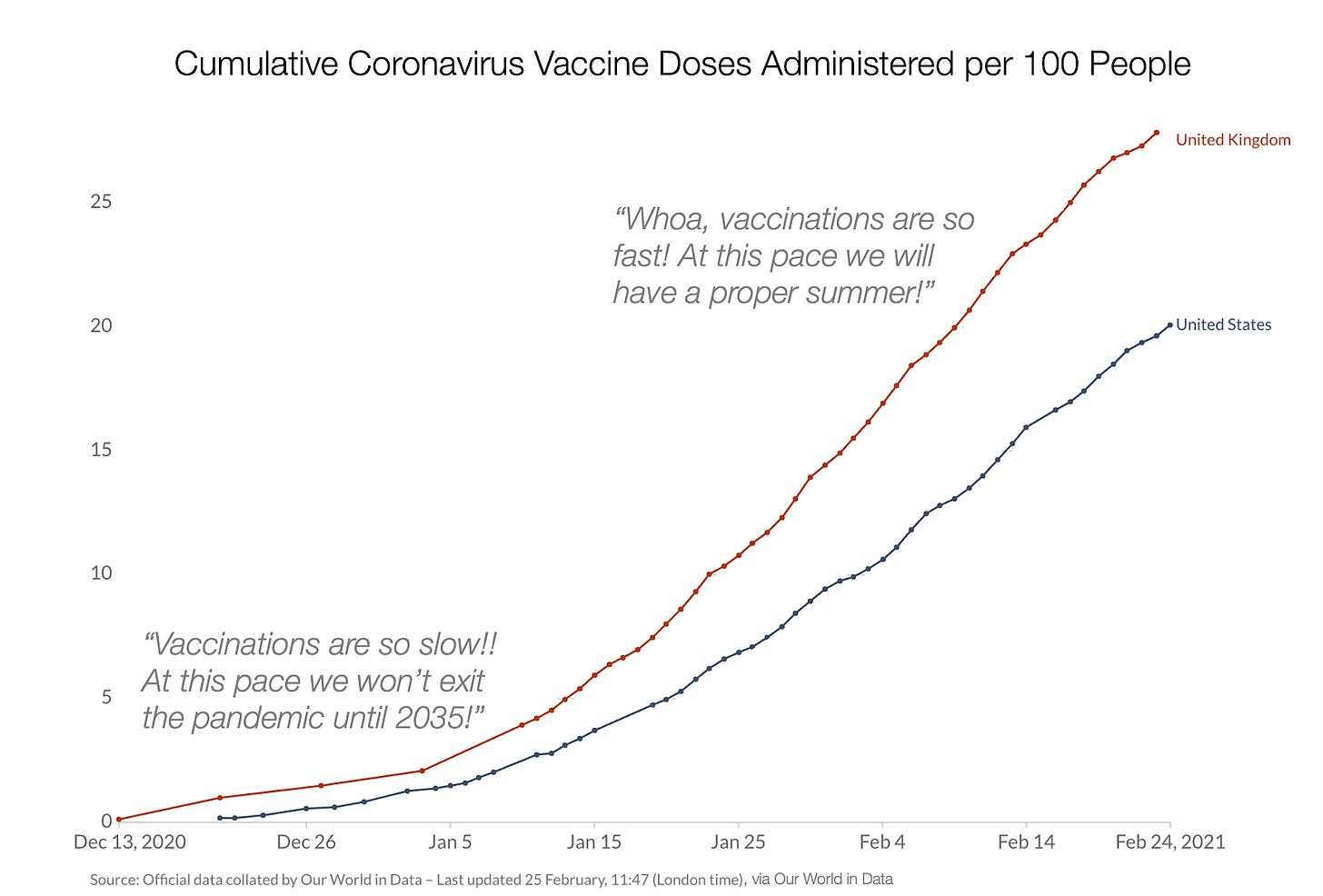
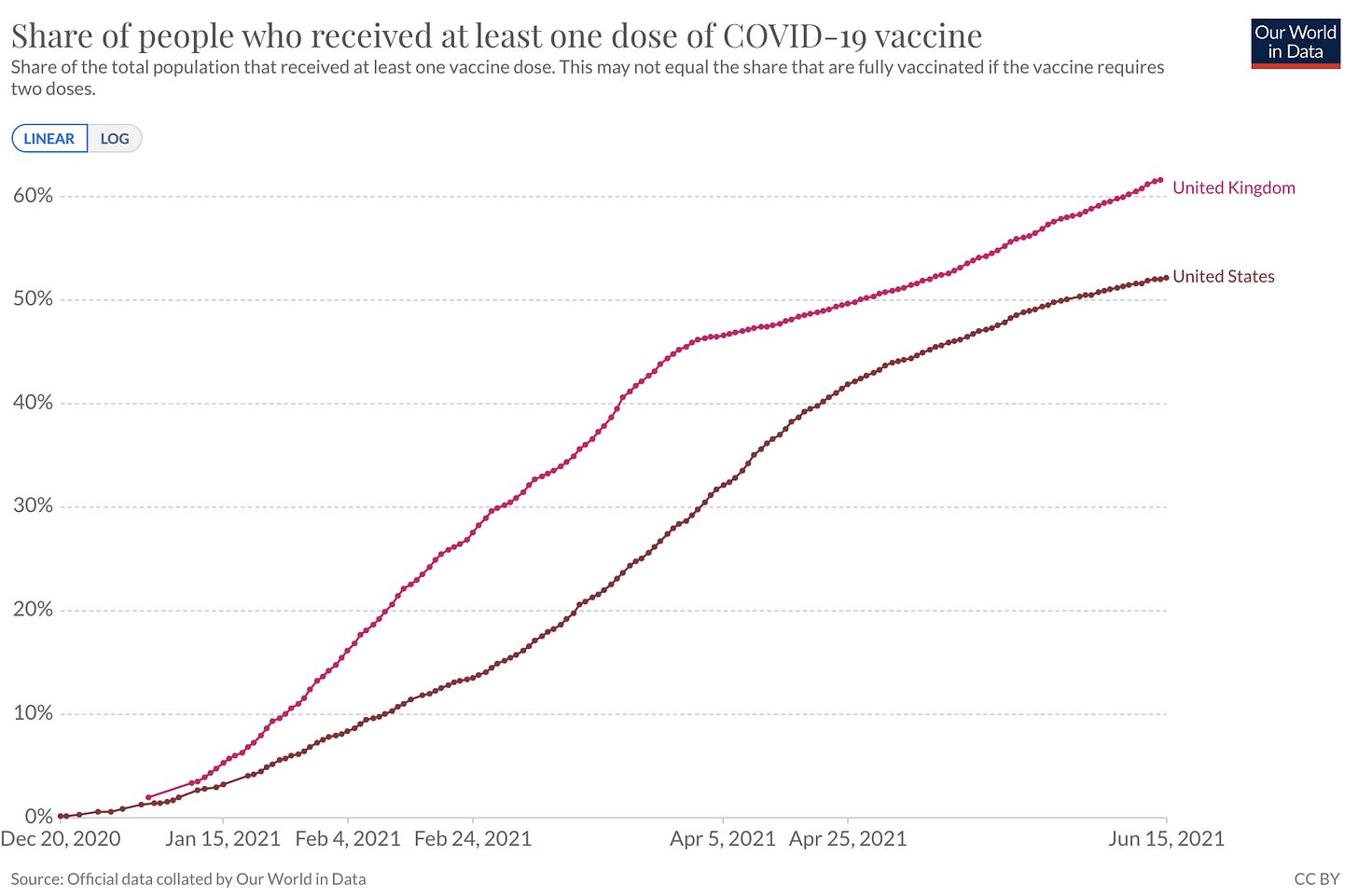
This sounds pretty simple, but amazingly most people are incapable of applying this idea to new areas! We saw this during the pandemic with vaccines: Every media outlet was alarmed at the sluggishness of vaccine rollout.
But what would happen was obvious if you thought about it in terms of S curves: Vaccinations, like any other business process, start slowly. As workers face the reality of distributing billions of doses, they identify problems, eliminate them, and little by little they improve every bottleneck until they are not the limiting factor to vaccinations anymore. They hit the invisible asymptote of nations not wanting to share vaccines, or parts of the population not willing to get vaccinated.
Any observer that keeps S curves in mind could have predicted that the vaccine situation would be getting better over time.
Sure enough:
Car speed and process improvements are good examples of approximately constant acceleration. If you see something that is constantly getting better, you are in front of an S curve.
A much faster growth than with linear acceleration is with organic acceleration.
Organic Acceleration
Imagine a cell reproducing. First there’s one cell that splits into two. The two split again, and become four. The four become eight, 16, 32, 64…
It works with tomatoes too1:
This exponential type of growth is called organic, because it’s driven by the size of the organism. The bigger the organism, the faster it grows2.
In epidemiology, this is represented by the famous R, the reproduction rate. For COVID, the worldwide average R0 of the first strain was 2.7, meaning that each infected person would infect 2.7 more. If you start with one infection, after 10 generations you have 20,000 cases, and after 10 more, over 400 million.
This is very counterintuitive. Before the pandemic, there were already famous games and stories that illustrated how important and counterintuitive this is.
For example, the story of the chess inventor and the Chinese emperor: To thank him for his invention of chess, the emperor asked him what he wanted in return. He proposed to get one grain of rice for the 1st square, two for the 2nd, four for the 3rd, eight for the 4th… It seemed little, so the emperor agreed.
But there are 8 rows of 8 squares on a chess board. That’s 64 squares. After the first two rows, he’d just get 1kg of rice. One more row gets to 210kg, or the weight of a pony. One more row is the size of a whale. The 5th row is a couple of navy destroyers. The 6th row is like 10 skyscrapers. By the 8th row, it’s a literal mountain worth of rice.
Another example is the famous riddle of the water lilies. The surface they occupy doubles in size each day, from 1 square meter to 2, 4, 8, etc. You observe them and they take 47 days to occupy half a pond. How many more days before they occupy all the pond?
The first reaction the majority has is to say 47 more days. The answer, of course, is one more day, since they double every day.
This is the reason why the world population has grown so fast over the last few centuries, why 7% of all the people in history are alive today.
The growth rate of the human population has been until now comparable to that of an epidemic. For COVID, we had the reproduction number R = 2.7, and the magic number to stop its spread is 1. For humans, we have the fertility rate. We say that the replacement rate—the magic number—is 2.1 children per woman3.
Ideas also grow organically: Each person shares an article or video with X people, who then share it with X other people each, and so on. That’s how an article can get to 40 million views, or QAnon can spread to 10% of Americans.
If you identify something that grows based on its size, you are experiencing exponential acceleration.
Threshold Acceleration
Yet another type of S curve growth happens through thresholds: a minimum amount of something is required for a process to happen.
Take an ice cube. In freezing temperatures, every molecule of water is moving, trying to escape, but they don’t have enough energy to break free their neighbor. You can heat it all you want, but it will still not be enough energy to melt it. That energy will spread through the ice cube, increasing the vibration of each water molecule.
But at some point, there’s enough energy for the molecules to break free. The ice cube starts melting. If one molecule gets warmer, it will move a lot, and pass that energy back to another water molecule that is still iced, bringing the original temperature back down to 0°C and liquefying the iced molecules.
Both neurons and transistors fire the same way: if they receive a little bit of energy, they don’t do anything. But send them enough and they will fire all in.
If you think about it, the same thing happens with your thoughts. You have many of them going through your mind, but you let most of them go. But if they pass a threshold of good enough, you will write them down or say them out loud.
This is how countries get formed: Pent-up tension reaches a point where it explodes, generating a war or revolution that changes the geographic map.
It’s also how marketplaces work online. For example, Uber couldn’t just open a new city welcoming drivers and riders: If there’s not enough drivers, riders will open the app, see there’s nobody available, close it, and never open it again. Drivers won’t see many riders, so they won’t start driving.
This is called the cold start problem. The way it’s resolved is by artificially adding one side of the marketplace—usually supply. In the case of Uber, when they opened a new city, they first agreed with drivers to start driving a given day, while they did a huge marketing campaign to let riders know. Once riders and drivers have passed the threshold, there’s enough of them to keep growing in the city as more drivers and riders experience a well-functioning app.
If you identify something that can become an S-curve but hasn’t yet because it hasn’t reached a threshold, you might have an opportunity: figure out a way to cross the threshold, and harvest the benefits of its growth.
Hypergrowth Phase
When something is in hypergrowth, it’s growing faster than it’s ever been. This is when healthcare systems collapse during a pandemic, or when hypergrowth companies can’t cope with all the ways they’re breaking at the seams.
But this phase betrays a fact: it’s the end of the beginning.
Let’s take something we’re all now used to: cumulative and new cases. When cumulative cases are growing fastest, new cases have peaked and are starting to go down.
We understand this well because we’ve been seeing these curves for a year and a half. But it’s not always as intuitive. For example, companies might be too busy handling problems to realize that their growth is slowing down and they need to prepare for the next phase: deceleration.
Deceleration and Invisible Asymptotes
When you’re dealing with something that is growing exponentially, it can’t last forever. It will slow down at some point, and then slow down more and more as it gets closer to the asymptote. Why?
Although there’s many ways for an S curve to accelerate, there’s one main way to decelerate: saturation, when there’s nothing left to keep growing.
It’s what happens when there’s no more ice to melt, no more riders interested in Uber in a city, no more food for a population to keep growing, when herd immunity has been reached, when the car arrives home, when everybody’s been vaccinated, when the neuron has already fired, when everybody on earth has a bit of Bitcoin…
When you’re in growth mode, you might not see the slowdown coming, but you need to know it’s there, even if the asymptote is invisible. You must figure out a way to know where it stands to make decisions.
For example, in epidemiology the herd immunity threshold tells you when the epidemic will start really dying down. The early number was ~60%. Knowing that allowed epidemiologists to calculate how many people would die if the virus was let to run loose (~60% * 1% fatality rate = 0.6% of the population dead, not counting new variants, collateral damage, or long COVID). That number allowed the public to decide whether that was acceptable or not.
In companies, you want to assess the invisible asymptote while you’re still growing fast. If you’re short on resources and still far away from the asymptote, focus on your current business. But if you start having resources and are getting closer to the invisible asymptote, it’s time to invest in creating a new S curve.
How Can You Use S Curves
Seeing S curves will help you predict things better in business and life:
It’s not enough to know something is growing fast. You want to know it’s growing faster and faster. For example, if you are considering joining a hypergrowth company, it’s crucial to know how they’re growing. If it’s through advertising, for example, that does not tend to compound. The opposite: the more you invest, the more expensive it gets and the worse the clients you get.
Conversely, if you have tapped into organic growth, it’s time to be persistent and, if you can, go big. 10% growth week over week is 140x over one year. Don’t worry if the absolute amounts are still small (eg, “Oh it’s just growing at $10k per month”… “Yeah, but that’s 100% month over month for the past 3 months, completely organically!”).
Conversely, beware of these organic growths. One day you might think your competitors are small and weak, and the next they beat you (ask MySpace). Or you might think a new pandemic is no big deal and…
Every exponential growth will eventually saturate. To predict the slowdown, understand where the invisible asymptote is. To do that, understand who is the target of that growth, and assess how many people like that there are.
If the invisible asymptote is far away and you have few resources, keep focusing on improving your current business. If you have substantial resources or the invisible asymptote is getting closer, start investing in new S curves.
S curves can stack. Find a new path for growth to add a new S curve.
When you’re thinking about where to invest, pay attention to early S curves. For example, aggregators are types of companies that have network effects, so if they reach critical mass they will grow exponentially after that. Google, Facebook, Shopify, Uber, Youtube, Airbnb… All aggregators.
This is a joke, both on my side and Nick Huber’s. Letting you know just in case. Apparently Twitter doesn’t understand irony.
In biology, this is represented by the famous formula dy/dt=ky, where the change of something over time (dy/dt) depends on the size of that thing (y), multiplied by some constant.
Why is the replacement rate 2.1 instead of 1 like for R in epidemics? Let’s take 100 women. They need at least 200 children to get 100 girls that replace them, the rest being boys.
Why is the replacement rate 2.1 and not 2.0? There are 2 reasons. The first one is that there’s actually 105 boys born for every 100 girls. So 100 women need to have 205 children to get 100 girls. The second factor is mortality. Depending on how the fertility is calculated, statisticians might consider only the children had by women 15 years old and older. But if a girl dies between her birth and her 15th birthday, she needs to be replaced. If 100 women have 2.1 children each, they get ~102.4 girls. Let’s say child mortality is 2%. So only ~100 girls will reach 15 years old. To give you some orders of magnitude, the current mortality rate for girls 0-15 years old is ~0.6% in the US, and ~4% globally.

















S-curve is basically a cumulative curve of the bell curve. So , like in marketing or innovation, first (Bell curve) we have innovators, then early adopters, then early majority - inflection point) , then late majority and laggards. In cumulative terms one gets S-curve. Another interesting story is time of transition from one S-curve to another . Like transition from vacuum lamps to transistors , etc. Or ICE to EV vehicles.
A long time ago - early to mid-50s, I think - Prof. Jay Forrester at MIT came up with the "bullwhip" or "whiplash" effect (later termed as the Forrester effect). This referred to very small perturbations (say, 2%) in customer purchases at checkout of specific products that cycled back through the entire supply chain in ever increasing amounts. What he evidenced was the increasing amplitude of demand-generated effects on supply all the way back through upstream vendors.
He theorized that the initial small dip or increase in sales of a particular item (itself possibly random) was subsequently misinterpreted by people in every preceding stage: first by the shelf replenishing clerk reporting to the store inventory head, who then inflated it some more while placing orders for the store at the local warehouse, that was then again inflated to the regional warehouse... And so on until it reached the manufacturer. The ripple effects took time and when the manufacturer finally increased production or invested in higher capacity, there was over-supply and unsold goods. All because the original blip at the checkout was just that: an inconsequential blip.
Of course, today's supply chain systems are architected for just-in-time using real time data. But the principles of human behaviours remain the same. And, for the purposes of this discussion, if one were to look backwards at the whiplash effect curve and smooth out the waveform, they do resemble the S curve - in reverse, or as mirror image.